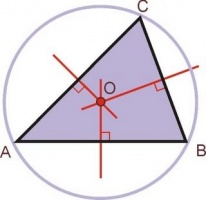
LOS LADOS DE LOS TRIANGULOS 

Clasificación de triángulos

• Por sus lados

• Por sus ángulos

Clasificación de triángulos según sus lados
Triángulo equilátero
Triángulo isósceles
Triángulo escaleno
Clasificación de triángulos según sus ángulos
Triángulo Rectángulo
Triángulo obtusángulo
Triángulo acutángulo
Triángulo equiángulo
Propiedades de los triángulos

Triángulos	Equilátero	Isósceles	Escaleno
Acutángulo
Rectángulo
Obstusángulo

• Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto, este triángulo es simétrico respecto de su altura diferente.

• Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene ejes de simetría.

• Triángulo rectángulo isósceles: con un angulo recto y dos agudos iguales (de  cada uno), dos lados son iguales y el otro diferente, naturalmente los lados iguales son los catetos, y el diferente es la hipotenusa, es simétrico respecto a la altura que pasa por el ángulo recto hasta la hipotenusa.

• Triángulo rectángulo escaleno: tiene un ángulo recto y todos sus lados y ángulos son diferentes.

• Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que parten del ángulo obtuso, el otro lado es mayor que estos dos.

• Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.

Los tres delizadores Ladoa, Ladob y Ladoc son los lados del triángulo ABC con vértices en los puntos A, B y C. Active la
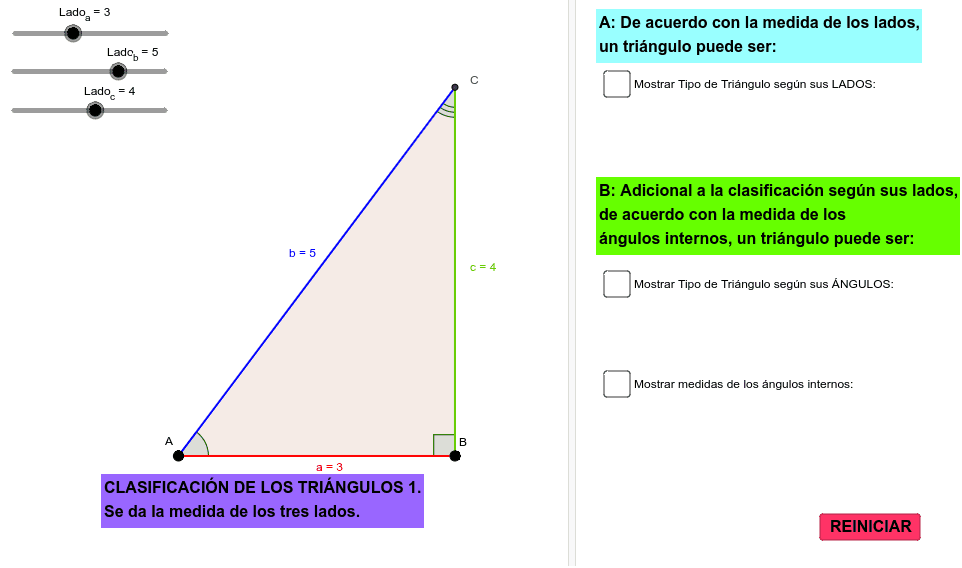
Active la casilla de verificación de la parte A y modifique la medida de uno o más lados: Observe la clase de triángulo que se forma en cada caso. También puede activar las
También puede activar las casillas de verificación de la parte B y analizar las medidas de los ángulos interiores y la clase de triángulo de acuerdo con sus ángulos.
La relación entre las medidas de los tres lados del triángulo determina la clasificación en Triángulo Equilátero, Triángulo Isósceles y Triángulo Escaleno.
- Triángulo Equilátero: Las medidas de sus tres lados son iguales, es decir, los tres lados son congruentes. Etimológicamente, equi = igual; latero = lado.
- Triángulo Isósceles: Las medidas de dos lados son iguales, es decir, dos lados son congruentes. Etimológicamente, iso = igual; skeles = piernas.
- Triángulo Escaleno: Todas las medidas de sus lados son diferentes, es decir, no tiene lados congruentes. Etimológicamente, skalene = oblicuo. Cada uno de los ángulos interiores del triángulo puede ser ángulo agudo (si es menor de 90°), ángulo recto (si es igual a 90°) o ángulo obtuso (si es mayor de 90° pero menor de 180°). Con base en los ángulos interiores, los triángulos se clasifican en Triángulo Acutángulo, Triángulo Rectángulo y Triángulo Obtusángulo.
Triángulo Acutángulo: Cuando los tres ángulos interiores son agudos. Triángulo Rectángulo: Cuando un ángulo es recto. Triángulo Obtusángulo: Cuando un ángulo es obtuso. Así las cosas, Así las cosas, todo triángulo recibe dos nombres, uno por cada clasificación. Por lo tanto se pueden tener los siguientes triángulos: - Triángulo equilátero-acutángulo (también se llama equiángulo).
- Triángulo isósceles-acutángulo.
- Triángulo isósceles-rectángulo.
- Triángulo isósceles-obtusángulo.
- Triángulo escaleno-acutángulo.
- Triángulo escaleno-rectángulo.
- Triángulo escaleno-obtusángulo. Algunas propiedades de los triángulos:
- La suma de las medidas de los ángulos interiores es igual a 180° o ángulo llano.
- Si dos lados son congruentes entonces el triángulo tiene dos ángulos congruentes.
- A lado mayor se opone el ángulo mayor y al lado menor se opone el ángulo menor.
- Si un triángulo tiene dos ángulos congruentes entonces es triángulo isósceles.
- El lado mayor del triángulo siempre es de menor medida que la suma de las medidas de los otros dos lados: Si los lados del triángulo son a, b, c y c es el lado mayor, entonces c < a + b. - En todo triángulo rectángulo los otros dos ángulos son agudos. - En todo triángulo obtusángulo los otros dos ángulos son agudos.
- En todo triángulo rectángulo los otros dos ángulos son agudos.
- En todo triángulo obtusángulo los otros dos ángulos son agudos.

Los triángulos se pueden clasificar según diferentes criterios:

Si sus tres lados tienen la misma longitud (los tres ángulos internos miden grados).

Si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.

Si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.

Si tiene un ángulo interior recto . A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.

Si uno de sus ángulos es obtuso (mayor de ); los otros dos son agudos (menor de ).

Cuando sus tres ángulos son menores a ; el triángulo equilátero es un caso particular de triángulo acutángulo.

Normalmente se llama triángulo equilátero y ya se ha comentado anteriormente.

Podemos ver en el esquema anterior que las clasificaciones comentadas en el apartado anterior se pueden combinar de dos a dos (una de cada apartado).

Así, tenemos las siguientes características:

Los triángulos rectángulos pueden ser:

Los triángulos obtusángulos son:

                                 

PUNTOS DE UN TRIANGULO

Rectas y puntos notables de un triángulo. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. En los triángulos se puede denotar un grupo de rectas y puntos muy importantes. Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

                                

Sumario

 [ocultar] 

• 1 Mediatriz
  • 1.1 Mediatrices de un triángulo obtusángulo
  • 1.2 Meditrices de un triángulo rectángulo
• 2 Mediana
• 3 Las Alturas
  • 3.1 El ortocentro en un triangulo obtusángulo
• 4 Las bisectrices
• 5 Generalidades
• 6 Fuentes
•              
•  

Mediatriz

                               

Mediatriz: Conjunto de puntos del plano que equidistan de los puntos extremos de un segmento. Como consecuencia la mediatriz biseca perpendicularmente al segmento.

 En un triángulo, las tres mediatrices de sus lados concurren en un punto que equidista de los vértices del triángulo. El punto en el que se cortan las mediatrices de un triángulo, se conoce como circuncentro, o sea, el centro de la circunferencia circunscrita al triángulo de referencia. Al radio de la circunferencia circunscrita se le suele llamar circunradio y es la distancia desde el circuncentro a los vértices del triángulo. Obviando el rigor de la definición de círculo, a la circunferencia circunscrita se le llama también circuncírculo (para abreviar).

mediatríz

• En el triángulo ABC las mediatrices MAC, MBC y MAB se intersecan en el punto C que costituye el circucentro del triángulo o centro de la circunferencia circunscrita al triángulo ABC.

Mediatrices de un triángulo rectángulo

Mediatrices de un triángulo obtusángulo

• En el caso de los triángulos obtusángulos, el circuncentro es un punto ubicado fuera del triángulo.

Mediatrices de un triángulo obtusángulo

Meditrices de un triángulo rectángulo

• En el caso de los triángulos rectángulos, el circuncentro es el punto medio de la hipotenusa

Mediana

Mediana:

                                

• La mediana es el segmento de recta que se traza desde un vértice de un triángulo al punto medio de su lado opuesto.
• Las tres medianas de un triángulo concurren en un punto.
• El punto donde se cortan la medianas de un triángulo se conoce como baricentro, centroide o centro de gravedad y tiene una propiedad física muy importante: Si colocamos un eje a través de él y dejamos libre el triángulo, este no se mueve por acción de la aceleración de la gravedad, es por ello que el baricentro se llama centro de gravedad del triángulo.
• Las medianas se cortan siempre en un punto interior al triángulo.
• El baricentro divide a cada mediana en la razón 2:1. Esto es, la longitud del segmento de mediana medida desde el vértice al baricentro es el doble que desde el baricentro al punto medio del lado en cuestión.
• Cada mediana de un triángulo, lo divide en dos triángulos de igual área.

Mediana

Las Alturas

• Se llama altura de un triángulo al segmento de perpendicular trazada por un vértice del triángulo y comprendido entre ese vértice y su lado opuesto.

• Las alturas de un triángulo concurren en un punto denominado ortocentro del triángulo.

• El ortocentro de un triángulo acutángulo es un punto interior del triángulo.

El ortocentro en un triangulo obtusángulo

• En el caso de un triángulo obtusángulo, el ortocentro es un punto exterior al triángulo.

Archivo:Ortocentro obtusangulo.JPG

• En el caso del triángulo rectángulo vemos que el ortocentro coincide con el vértice del ángulo recto.

• Los pies de las alturas de un triángulo determinan un triángulo llamado: triángulo pedal u órtico del triángulo dado.

Las bisectrices

• Bisectriz de un ángulo: Es el conjunto de puntos del plano donde está contenido el ángulo que equidista de los lados del ángulo. Como consecuencia la bisectriz de un ángulo lo divide en dos ángulos de igual amplitud.

• Todo ángulo tiene dos bisectrices, una interna y otra externa. Las bisectrices interna y externa de un ángulo son perpendiculares entre sí.

• Las bisectrices de los ángulos interiores de un triángulo concurren en un punto que equdista de los lados del triángulo, llamado incentro del triángulo o centro de la circunferencia inscrita en el triánguloy siempre es interior al triángulo. La equidistancia se llama inradio o radio de la circunferencia inscrita en el triángulo.

• Cada bisectriz interna y las bisectrices de los otros dos ángulos externos del triángulo concurren en otros tres puntos que también equidistan de los lados (o sus prolongaciones) del triángulo. Estos puntos se llaman exincentros del triángulo y las circunferencias que determinan: circunferencias exinscritas del triángulo. Algunos autores las llaman circunferencias excritas o excírculos y a sus centros excentros.

Generalidades

• Una ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto a este. También se la conoce como transversal angular.La mediana, la altura y la bisectriz son cevianas. El nombre de ceviana fue introducido por M.A. Poulain, que lo introdujo en honor de Giovanni Ceva, quien en 1678 había formulado el teorema que lleva su nombre: Teorema de Ceva. Este teorema da la condición necesaria y suficiente para que tres cevianas se corten en un punto.

• En el triángulo equilátero coinciden todas las rectas y puntos notables tratados, es decir, las medianas, las alturas, las bisectrices y las mediatrices, así como el baricentro, el ortocentro, el incentro y el circuncenro.

• En el triángulo isósceles la altura relativa a la base, es mediana, bisectriz y mediatriz.

• El ortocentro de un triángulo coincide con el incentro de su triángulo pedal.

• Se conoce como circunferencia de los nueve puntos a una circunferencia que se puede construir sobre cualquier triángulo dado. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (excepto que el triángulo sea obtusángulo). Estos nueve puntos son: el punto medio de cada lado del triángulo, los pies de las alturas, y los puntos medios de los segmentos determinados por el ortocentro y los vértices del triángulo. A la circunferencia de los nueve puntos se le conoce también entre otros como circunferencia de Feuerbach, circunferencia de Euler, etc.

• Existen otras rectas y puntos notables del triángulo, a saber:

• La recta de Simson, las simedianas y puntos simedianos,, punto, ángulo y circunferencia de Brocard, la recta de Gauss, el punto de Miquel, la circunferencia de Lemoine, etc.

• Son teoremas importantes relacionados con las rectas y puntos notables del triaángulo, colinealidad de puntos o concurrencia de rectas, los teoremas Carnot, de Ceva, de Menelao, de Feuerbach, de Desargues, de Stewart, de Steiner, de Spieker, etc.

BÉLICES Y ALTURAS 

La altura de un triángulo es el segmento perpendicular a un lado que va desde el vértice opuesto a este lado (o a su prolongación). También puede entenderse como la distancia de un lado al vértice opuesto.

Hay tres alturas (h_a, h_b y h_c), según a que lado está asociada dicha altura. A partir de la fórmula de Herón, conociendo los tres lados (a, b y c), se pueden hallar las tres alturas:

Las tres alturas del triángulo (o sus prolongaciones) se cortan en un punto llamado ortocentro (H).

Las alturas podrían estar en el exterior del triángulo, en el caso de que sea un triángulo obtusángulo. El ortocentro también será exterior en los triángulos obtusángulos. En los rectángulos coincidirá con el vértice del ángulo recto. En los acutángulos, será un punto interior.

Altura de un triángulo equilátero

ANUNCIOS

La altura (h) del triángulo equilátero se puede calcular a partir del teorema de Pitágoras. Los lados a, a/2 y h forman un triángulo rectángulo. Los lados a/2 y h son los catetos y a la hipotenusa.

Aplicando el teorema de Pitágoras:

Y obtenemos que la altura (h) del triángulo equilátero es:

Otro procedimiento para calcular su altura sería a partir de las razones trigonométricas.

Respecto al ángulo de 60º, la razón entre la altura h y la hipotenusa del triángulo a es igual al seno de 60º. Por tanto:

Altura de un triángulo isósceles

La altura (h) del triángulo isósceles se puede calcular a partir del teorema de Pitágoras. Los lados a, b/2 y h forman un triángulo rectángulo. Los lados b/2 y h son los catetos y a la hipotenusa.

Por el teorema de Pitágoras:

Y se obtiene que la altura h es:

En un triángulo isósceles, la altura correspondiente a la base (b) es también la bisectriz, mediatriz y mediana.

Altura de un triángulo rectángulo

Las alturas del triángulo rectángulo asociadas a los catetos (a y b) son el cateto opuesto. Por lo tanto, h_a=b y h_b=a.

Ejercicio

Para calcular la altura asociada al lado c (la hipotenusa) se recurre al teorema de la altura.

La altura h (o h_c) puede obtenerse conociendo los tres lados del triángulo rectángulo.

Sea un triángulo con los tres lados conocidos, siendo estos a=3 cm, b=4 cm y c=4.5 cm.

¿Cuales son sus alturas h_a, h_b y h_c? Primero calcularemos el semiperímetro (s).

Obtenemos que el semiperímetro es s=5,75 cm. Ahora podemos calcular las tres alturas

Y las tres alturas serán h_a=3,92 cm, h_b=2,94 cm y h_c=2,61 cm.