
CAMBIAR LAS UNIDADES DE VELOCIDAD
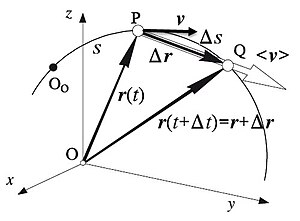
La velocidad es la magnitud física de carácter vectorial que relaciona el cambio de posición (o desplazamiento) con el tiempo. Se representa con: o (en la escritura manuscrita). En análisis dimensional sus dimensiones son: [L]/[t].12 Su unidad en el Sistema Internacional de Unidades es el metro por segundo(símbolo, m/s).
En virtud de su carácter vectorial, para definir la velocidad debe considerarse la dirección del desplazamiento y el módulo, el cual se denomina celeridad o rapidez.3
Aristóteles estudió los fenómenos físicos sin llegar a conceptualizar una noción de velocidad. En efecto, sus explicaciones (que posteriormente se demostrarían incorrectas) solo describían los fenómenos inherentes al movimiento sin usar las matemáticas como herramienta.
Fue Galileo Galilei quien, estudiando el movimiento de los cuerpos en un plano inclinado, formuló el concepto de velocidad. Para ello, fijó un patrón de unidad de tiempo, como por ejemplo 1 segundo, y midió la distancia recorrida por un cuerpo en cada unidad de tiempo. De esta manera, Galileo desarrolló el concepto de la velocidad como la distancia recorrida por unidad de tiempo. A pesar del gran avance que representó la introducción de esta nueva noción, sus alcances se limitaban a los alcances mismos de las matemáticas. Por ejemplo, era relativamente sencillo calcular la velocidad de un móvil que se desplazase a velocidad constante, puesto que en cada unidad de tiempo recorre distancias iguales. También lo era calcular la velocidad de un móvil con aceleración constante, como es el caso un cuerpo en caída libre. Sin embargo, cuando la velocidad del objeto variaba de forma más complicada, Galileo no disponía de herramientas matemáticas que le permitiesen determinar la velocidad instantánea de un cuerpo.
Fue recién en el siglo XVI, con el desarrollo del cálculo por parte de Isaac Newton y Gottfried Leibniz, cuando se pudo solucionar la cuestión de obtener la velocidad instantánea de un cuerpo. Esta está determinada por la derivada del vector de posición del objeto respecto del tiempo.
Las aplicaciones de la velocidad, con el uso de Cálculo, es una herramienta fundamental en Física e Ingeniería, extendiéndose en prácticamente todo fenómeno que implique cambios de posición respecto del tiempo, esto es, que implique movimiento.
Un término relacionado con la velocidad es el de celeridad. En el lenguaje cotidiano empleamos frecuentemente el término velocidad para referirnos a la celeridad . En física hacemos una distinción entre ellas, ya que la celeridad es una magnitud escalar que representa el módulo de la velocidad. De manera muy sencilla, si decimos que una partícula se mueve con una velocidad de 10 m/s, nos estamos refiriendo a su celeridad; por el contrario, si además especificamos la dirección en que se mueve, nos estamos refiriendo a su velocidad.
Fuerza de rozamiento por deslizamiento
En la figura, se muestra un bloque arrastrado por una fuerza F horizontal. Sobre el bloque actúan el peso mg, la fuerza normal N que es igual al peso, y la fuerza de rozamiento Fk entre el bloque y el plano sobre el cual desliza. Si el bloque desliza con velocidad constante la fuerza aplicada F será igual a la fuerza de rozamiento por deslizamiento Fk.
roza4.gif (1024 bytes)
Podemos investigar la dependencia de Fk con la fuerza normal N. Veremos que si duplicamos la masa m del bloque que desliza colocando encima de éste otro igual, la fuerza normal N se duplica, la fuerza F con la que tiramos del bloque se duplica y por tanto, Fk se duplica.
La fuerza de rozamiento por deslizamiento Fk es proporcional a la fuerza normal N.
Fk=mk NLa constante de proporcionalidad mk es un número sin dimensiones que se denomina coeficiente de rozamiento cinético.
El valor de mk es casi independiente del valor de la velocidad para velocidades relativas pequeñas entre las superficies, y decrece lentamente cuando el valor de la velocidad aumenta.
Publicado 10th April 2013 por titian
0 Añadir un comentario
APR
10
fuerza normal
La fuerza normal
La fuerza normal, reacción del plano o fuerza que ejerce el plano sobre el bloque depende del peso del bloque, la inclinación del plano y de otras fuerzas que se ejerzan sobre el bloque.
roza1.gif (916 bytes) Supongamos que un bloque de masa m está en reposo sobre una superficie horizontal, las únicas fuerzas que actúan sobre él son el peso mg y la fuerza y la fuerza normal N. De las condiciones de equilibrio se obtiene que la fuerza normal N es igual al peso mgN=mg
Si ahora, el plano está inclinado un ángulo q , el bloque está en equilibrio en sentido perpendicular al plano inclinado por lo que la fuerza normal N es igual a la componente del peso perpendicular al plano, N=mg·cosq
Consideremos de nuevo el bloque sobre la superficie horizontal. Si además atamos una cuerda al bloque que forme un ángulo q con la horizontal, la fuerza normal deja de ser igual al peso. La condición de equilibrio en la dirección perpendicular al plano establece N+ F·senq =mg
Publicado 10th April 2013 por titian
0 Añadir un comentario
APR
10
fisica para los estudiantes

Explicación del origen del rozamiento por contacto
La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.
Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se produzca. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.
Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que haya en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente de rozamiento cinético es menor que el coeficiente de rozamiento estático.
Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.
La explicación de que la fuerza de rozamiento es independiente del área de la superficie aparente de contacto es la siguiente:
roza7.gif (2712 bytes)
En la figura, la superficie más pequeña de un bloque está situada sobre un plano. En el dibujo situado arriba, vemos un esquema de lo que se vería al microscopio: grandes deformaciones de los picos de las dos superficies que están en contacto. Por cada unidad de superficie del bloque, el área de contacto real es relativamente grande (aunque esta es una pequeña fracción de la superficie aparente de contacto, es decir, el área de la base del bloque).
roza8.gif (2712 bytes)
En la figura, la superficie más grande del bloque está situada sobre el plano. El dibujo muestra ahora que las deformaciones de los picos en contacto son ahora más pequeñas por que la presión es más pequeña. Por tanto, un área relativamente más pequeña está en contacto real por unidad de superficie del bloque. Como el área aparente en contacto del bloque es mayor, se deduce que el área real total de contacto es esencialmente la misma en ambos casos.
Ahora bien, las investigaciones actuales que estudian el rozamiento a escala atómica demuestran que la explicación dada anteriormente es muy general y que la naturaleza de la fuerza de rozamiento es muy compleja (Véase el artículo titulado "Rozamiento a escala atómica" en la bibliografía de este capítulo.
Publicado 10th April 2013 por titian
1 Ver comentarios
APR
10
transformaciones de unidades
TRANSFORMACIONES DE UNIDADES
En muchas situaciones en Física, tenemos que realizar operaciones con magnitudes que vienen expresadas en unidades que no son homogéneas. Para que los cálculos que realicemos sean correctos, debemos transformar las unidades de forma que se cumpla el principio de homogeneidad.
Por ejemplo, si queremos calcular la distancia recorrida por un móvil que se mueve a velocidad constante de 72 Km/h en un trayecto que le lleva 30 segundos, debemos aplicar la sencilla ecuación d = v·t, pero tenemos el problema de que la velocidad viene expresada en kilómetros/hora, mientras que el tiempo viene en segundos. Esto nos obliga a transformar una de las dos unidades, de forma que ambas sean la misma, para no violar el principio de homogeneidad y que el cálculo sea acertado.
Para realizar la transformación utilizamos los factores de conversión. Llamamos factor de conversión a la relación de equivalencia entre dos unidades de la misma magnitud, es decir, un cociente que nos indica los valores numéricos de equivalencia entre ambas unidades

Es muy importante en Física poder realizar la transformación de unidades, es decir expresar una magnitud en unidades equivalentes.
Las unidades para ser equivalentes deben ser homogéneas o de la misma especie. Por ejemplo: una longitud puede medirse en metros, centímetros, pies, kilómetros etc., pero no en kilogramos o en segundos. Metros, centímetros, pies etc. son unidades homogéneas o de la misma especie porque existe entre ellas una relación de equivalencia: (1 m. = 100 cm. = 3.28 pies).
Metro, kilogramo y segundo son unidades heterogéneas o de diferente especie porque no existe entre ellas relación de equivalencia (1m. no es igual a ninguna cantidad de Kg. o de segundos).
La transformación de unidades sólo puede llevarse a cabo entre unidades de la misma especie que la magnitud medida.
Una longitud dada en centímetros o en pies puede expresarse en metros o en kilómetros. Una masa dada en gramos o en libras masa, puede expresarse en kilogramos o toneladas.
EJERCICIOS.
Efectúa las siguientes transformaciones:
a.- 140 Km/h a m/s
140 Km * 1000m * 1 h = 38,8 m/s
h 1 Km 3600 s
b.- 95 Km/h a cm/s
95 Km * 1000m *100 cm * 1 h = 2638,8 m/s
h 1 Km 1 m 3600 s
c.- 1,5 cm/s a m/s
1,5 cm * 1 m = 0,015 m/s
s 100 cm
d.- a.- 50 cm/min2 a m/s2
50 cm * 1 m * 1 min2 = 0,000138 m/s2
min2 100 cm (60 s)2
e.- 0,5 Km/h2 a m/s2
0,5 Km * 1000m * 1 h2 = 0,000038 m/s2
h2 1 Km (3600)s2
f.- 200 cm/s a Km/h
200 cm * 1 m * 1 Km * 3600 s = 7,2 Km/h
s 100 cm 1000m 1 h
g) Ordena en forma creciente, los siguientes valores de rapidez: 40 Km/h; 120 m/s ; 12 Km/s y 180 cm/s.
40 Km * 1000 m * 1 h = 11,11 m/s
h 1 Km 3600 s
12 Km * 1 Km * 1 h = 3,33 m/s
h 1000 m 3600 s
180 cm * 1 m = 1,8 m/s
s 100 cm
1,8 m/s < 3,33 m/s<11,11 m/s <120 m/s

h) Ordena em forma decreciente cada uno de los siguientes valores de aceleración: 2 cm/s2 ; 0,0004 m/s2y 36.108 Km/min2
2 cm/s2 a m/s2
2 cm * 1 m = 0,02 m/s2
s2 100 cm
36.108 Km/min2 a m/s2
36.108 Km * 1000 m * 1 min2 = 1.109 m/s2
min2 1 Km (60 s)2
1.109 m/s2 >0,0004 m/s2> 0,02 m/s2
UNIDAD 2. MOVIMIENTO RECTILINEO UNIFORME VARIADO
Movimiento: Un cuerpo esta en movimiento cuando suposición varia con el tiempo con respecto a un punto que se considera fijo.
Uniformemente Variado: Es aquel cuya rapidez varía (aumenta o disminuye). Una cantidad constante en cada unidad de tiempo, la aceleración representa la variación (aumento o disminución) de la rapidez un cada unidad de tiempo. Se caracteriza porque su trayectoria es una línea recta y el modulo de la velocidad varia proporcionalmente al tiempo. Por consiguiente, la aceleración normal es nula porque la velocidad varía uniformemente con el tiempo.
Rectilíneo: La trayectoria es una línea recta y el módulo de la velocidad varía proporcionalmente al tiempo.
Este movimiento puede ser acelerado si el modulo de la velocidad aumenta a medida que transcurre el tiempo y retardado si el modulo de la velocidad disminuye el transcurso del tiempo
Ejercicios:
a) ¿Qué rapidez inicial debería tener un móvil cuya aceleración es 2 m/s2, si debe alcanzar una rapidez de 108 Km/h a los 5 s de su partida?
Datos:
Vo=?
a= 2 m/s2
Vf=108 Km/h
t= 5 s
Transformaciones.
108 Km * 1000 m * 1 h = 30 m/s
h 1 Km 3600 s
Vf= Vo + a*t
Vo= Vf – a*t
Vo= 30 m/s - 2 m/s2 *5 s
Vo= 30 m/s – 10 m/s
Vo= 20 m/s
b) Un automóvil se desplaza con rapidez de 54 Km/h y debe detenerse en 1 s después que el conductor aplica los frenos. Calcular: a) La aceleración constante que los frenos le imprimen al automóvil b) la distancia recorrida por el
Datos:
Vo= 54 Km/h
t= 1 s
Vf =?
a=?
X=?
54 Km * 1000 m * 1 h = 15 m/s
h 1 Km 3600 s
a=Vf – Vo/t
a= 0 m/s – 15 m/s/1s
a= -15 m/s2
X=Vo*t + a*t2 /2
X=15 m/s * 1 s + (-15m/s2 )* (1s)2/2
X= 15 m – 7,5 m
X=7,5 m

c) Un cuerpo que parte del reposo se acelera a razón de 4 m/s2 durante 8 s, para luego moverse en movimiento uniforme durante 6 s y finalmente vuelve al reposo en 5 s. Calcular la distancia total recorrida.
Datos:
M.R.U.A
Vo= 0
a=4 m/s2
t= 8 s
X1=?
M.R.U
t= 6 s
X2=?
Vf=0
t=5 s
X3=?
Xtotal= ?
1er Movimiento:
M.R.U.A
Vo= 0
a=4 m/s2
t= 8 s
X1=?
X1= Vo*t + a*t2 /2
X1=0 m/s * 8 s + 4 m/s2 * (8s)2/2
X1= 0 m + 128 m
X1=128 m
Vf= Vo + a*t
Vf= 0 m/s + 4 m/s2 *8 s
Vf= 0 m/s + 32 m/s
Vf= 32 m/s
Esta Vf es la velocidad inicial del otro movimiento; ya que el movimiento es uniforme y la velocidad permanece constante
2do Movimiento:
M.R.U
X= V*t
X= 32 m/s * 6 s= 192 m
3er Movimiento:
Vo= 32 m/s
Vf= 0 m/s
t= 5 s
a=?
X3=?
a=Vf – Vo/t
a= 0 m/s – 32 m/s/5s
a= -6,4 m/s2
X3= Vo*t + a*t2 /2
X3=32 m/s * 5 s + (-6,4m/s2 )* (5s)2/2
X3= 160 m - 80 m
X3=80 m
Xtotal = X1 + X2 + X3
UNIDAD 3. CONDENSADORES
Definición , Unidades y Formulas:
En electricidad y electrónica, un condensador (del latín "condensare") es un dispositivo que almacenaenergía eléctrica, es un componente pasivo. Está formado por un par de superficies conductoras en situación de influencia total (esto es, que todas las líneas de campo eléctrico que parten de una van a parar a la otra), generalmente en forma de tablas, esferas o láminas, separadas por un material dieléctrico (siendo este utilizado en un condensador para disminuir el campo eléctrico, ya que actúa como aislante) o por elvacío, que, sometidas a una diferencia de potencial (d.d.p.) adquieren una determinada carga eléctrica, positiva en una de las placas y negativa en la otra (siendo nula la carga total almacenada).
La carga almacenada en una de las placas es proporcional a la diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad la llamada capacidad o capacitancia. En el Sistema internacional de unidades se mide en Faradios (F), siendo 1 faradio la capacidad de un condensador en el que, sometidas sus armaduras a una d.d.p. de 1 voltio, éstas adquieren una carga eléctrica de 1 culombio.
La capacidad de 1 faradio es mucho más grande que la de la mayoría de los condensadores, por lo que en la práctica se suele indicar la capacidad en micro- µF = 10-6, nano- nF = 10-9 o pico- pF = 10-12 -faradios
En la figura, se muestra un bloque arrastrado por una fuerza F horizontal. Sobre el bloque actúan el peso mg, la fuerza normal N que es igual al peso, y la fuerza de rozamiento Fk entre el bloque y el plano sobre el cual desliza. Si el bloque desliza con velocidad constante la fuerza aplicada F será igual a la fuerza de rozamiento por deslizamiento Fk.
roza4.gif (1024 bytes)
Podemos investigar la dependencia de Fk con la fuerza normal N. Veremos que si duplicamos la masa m del bloque que desliza colocando encima de éste otro igual, la fuerza normal N se duplica, la fuerza F con la que tiramos del bloque se duplica y por tanto, Fk se duplica.
La fuerza de rozamiento por deslizamiento Fk es proporcional a la fuerza normal N.
Fk=mk NLa constante de proporcionalidad mk es un número sin dimensiones que se denomina coeficiente de rozamiento cinético.
El valor de mk es casi independiente del valor de la velocidad para velocidades relativas pequeñas entre las superficies, y decrece lentamente cuando el valor de la velocidad aumenta.
Publicado 10th April 2013 por titian
0 Añadir un comentario
APR
10
fuerza normal
La fuerza normal
La fuerza normal, reacción del plano o fuerza que ejerce el plano sobre el bloque depende del peso del bloque, la inclinación del plano y de otras fuerzas que se ejerzan sobre el bloque.
roza1.gif (916 bytes) Supongamos que un bloque de masa m está en reposo sobre una superficie horizontal, las únicas fuerzas que actúan sobre él son el peso mg y la fuerza y la fuerza normal N. De las condiciones de equilibrio se obtiene que la fuerza normal N es igual al peso mgN=mg
Si ahora, el plano está inclinado un ángulo q , el bloque está en equilibrio en sentido perpendicular al plano inclinado por lo que la fuerza normal N es igual a la componente del peso perpendicular al plano, N=mg·cosq
Consideremos de nuevo el bloque sobre la superficie horizontal. Si además atamos una cuerda al bloque que forme un ángulo q con la horizontal, la fuerza normal deja de ser igual al peso. La condición de equilibrio en la dirección perpendicular al plano establece N+ F·senq =mg
Publicado 10th April 2013 por titian
0 Añadir un comentario
APR
10
fisica para los estudiantes

Explicación del origen del rozamiento por contacto
La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.
Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se produzca. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.
Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que haya en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente de rozamiento cinético es menor que el coeficiente de rozamiento estático.
Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.
La explicación de que la fuerza de rozamiento es independiente del área de la superficie aparente de contacto es la siguiente:
roza7.gif (2712 bytes)
En la figura, la superficie más pequeña de un bloque está situada sobre un plano. En el dibujo situado arriba, vemos un esquema de lo que se vería al microscopio: grandes deformaciones de los picos de las dos superficies que están en contacto. Por cada unidad de superficie del bloque, el área de contacto real es relativamente grande (aunque esta es una pequeña fracción de la superficie aparente de contacto, es decir, el área de la base del bloque).
roza8.gif (2712 bytes)
En la figura, la superficie más grande del bloque está situada sobre el plano. El dibujo muestra ahora que las deformaciones de los picos en contacto son ahora más pequeñas por que la presión es más pequeña. Por tanto, un área relativamente más pequeña está en contacto real por unidad de superficie del bloque. Como el área aparente en contacto del bloque es mayor, se deduce que el área real total de contacto es esencialmente la misma en ambos casos.
Ahora bien, las investigaciones actuales que estudian el rozamiento a escala atómica demuestran que la explicación dada anteriormente es muy general y que la naturaleza de la fuerza de rozamiento es muy compleja (Véase el artículo titulado "Rozamiento a escala atómica" en la bibliografía de este capítulo.
Publicado 10th April 2013 por titian
1 Ver comentarios
APR
10
transformaciones de unidades
TRANSFORMACIONES DE UNIDADES
En muchas situaciones en Física, tenemos que realizar operaciones con magnitudes que vienen expresadas en unidades que no son homogéneas. Para que los cálculos que realicemos sean correctos, debemos transformar las unidades de forma que se cumpla el principio de homogeneidad.
Por ejemplo, si queremos calcular la distancia recorrida por un móvil que se mueve a velocidad constante de 72 Km/h en un trayecto que le lleva 30 segundos, debemos aplicar la sencilla ecuación d = v·t, pero tenemos el problema de que la velocidad viene expresada en kilómetros/hora, mientras que el tiempo viene en segundos. Esto nos obliga a transformar una de las dos unidades, de forma que ambas sean la misma, para no violar el principio de homogeneidad y que el cálculo sea acertado.
Para realizar la transformación utilizamos los factores de conversión. Llamamos factor de conversión a la relación de equivalencia entre dos unidades de la misma magnitud, es decir, un cociente que nos indica los valores numéricos de equivalencia entre ambas unidades

Es muy importante en Física poder realizar la transformación de unidades, es decir expresar una magnitud en unidades equivalentes.
Las unidades para ser equivalentes deben ser homogéneas o de la misma especie. Por ejemplo: una longitud puede medirse en metros, centímetros, pies, kilómetros etc., pero no en kilogramos o en segundos. Metros, centímetros, pies etc. son unidades homogéneas o de la misma especie porque existe entre ellas una relación de equivalencia: (1 m. = 100 cm. = 3.28 pies).
Metro, kilogramo y segundo son unidades heterogéneas o de diferente especie porque no existe entre ellas relación de equivalencia (1m. no es igual a ninguna cantidad de Kg. o de segundos).
La transformación de unidades sólo puede llevarse a cabo entre unidades de la misma especie que la magnitud medida.
Una longitud dada en centímetros o en pies puede expresarse en metros o en kilómetros. Una masa dada en gramos o en libras masa, puede expresarse en kilogramos o toneladas.
EJERCICIOS.
Efectúa las siguientes transformaciones:
a.- 140 Km/h a m/s
140 Km * 1000m * 1 h = 38,8 m/s
h 1 Km 3600 s
b.- 95 Km/h a cm/s
95 Km * 1000m *100 cm * 1 h = 2638,8 m/s
h 1 Km 1 m 3600 s
c.- 1,5 cm/s a m/s
1,5 cm * 1 m = 0,015 m/s
s 100 cm
d.- a.- 50 cm/min2 a m/s2
50 cm * 1 m * 1 min2 = 0,000138 m/s2
min2 100 cm (60 s)2
e.- 0,5 Km/h2 a m/s2
0,5 Km * 1000m * 1 h2 = 0,000038 m/s2
h2 1 Km (3600)s2
f.- 200 cm/s a Km/h
200 cm * 1 m * 1 Km * 3600 s = 7,2 Km/h
s 100 cm 1000m 1 h
g) Ordena en forma creciente, los siguientes valores de rapidez: 40 Km/h; 120 m/s ; 12 Km/s y 180 cm/s.
40 Km * 1000 m * 1 h = 11,11 m/s
h 1 Km 3600 s
12 Km * 1 Km * 1 h = 3,33 m/s
h 1000 m 3600 s
180 cm * 1 m = 1,8 m/s
s 100 cm
1,8 m/s < 3,33 m/s<11,11 m/s <120 m/s

h) Ordena em forma decreciente cada uno de los siguientes valores de aceleración: 2 cm/s2 ; 0,0004 m/s2y 36.108 Km/min2
2 cm/s2 a m/s2
2 cm * 1 m = 0,02 m/s2
s2 100 cm
36.108 Km/min2 a m/s2
36.108 Km * 1000 m * 1 min2 = 1.109 m/s2
min2 1 Km (60 s)2
1.109 m/s2 >0,0004 m/s2> 0,02 m/s2
UNIDAD 2. MOVIMIENTO RECTILINEO UNIFORME VARIADO
Movimiento: Un cuerpo esta en movimiento cuando suposición varia con el tiempo con respecto a un punto que se considera fijo.
Uniformemente Variado: Es aquel cuya rapidez varía (aumenta o disminuye). Una cantidad constante en cada unidad de tiempo, la aceleración representa la variación (aumento o disminución) de la rapidez un cada unidad de tiempo. Se caracteriza porque su trayectoria es una línea recta y el modulo de la velocidad varia proporcionalmente al tiempo. Por consiguiente, la aceleración normal es nula porque la velocidad varía uniformemente con el tiempo.
Rectilíneo: La trayectoria es una línea recta y el módulo de la velocidad varía proporcionalmente al tiempo.
Este movimiento puede ser acelerado si el modulo de la velocidad aumenta a medida que transcurre el tiempo y retardado si el modulo de la velocidad disminuye el transcurso del tiempo
Ejercicios:
a) ¿Qué rapidez inicial debería tener un móvil cuya aceleración es 2 m/s2, si debe alcanzar una rapidez de 108 Km/h a los 5 s de su partida?
Datos:
Vo=?
a= 2 m/s2
Vf=108 Km/h
t= 5 s
Transformaciones.
108 Km * 1000 m * 1 h = 30 m/s
h 1 Km 3600 s
Vf= Vo + a*t
Vo= Vf – a*t
Vo= 30 m/s - 2 m/s2 *5 s
Vo= 30 m/s – 10 m/s
Vo= 20 m/s
b) Un automóvil se desplaza con rapidez de 54 Km/h y debe detenerse en 1 s después que el conductor aplica los frenos. Calcular: a) La aceleración constante que los frenos le imprimen al automóvil b) la distancia recorrida por el
Datos:
Vo= 54 Km/h
t= 1 s
Vf =?
a=?
X=?
54 Km * 1000 m * 1 h = 15 m/s
h 1 Km 3600 s
a=Vf – Vo/t
a= 0 m/s – 15 m/s/1s
a= -15 m/s2
X=Vo*t + a*t2 /2
X=15 m/s * 1 s + (-15m/s2 )* (1s)2/2
X= 15 m – 7,5 m
X=7,5 m

c) Un cuerpo que parte del reposo se acelera a razón de 4 m/s2 durante 8 s, para luego moverse en movimiento uniforme durante 6 s y finalmente vuelve al reposo en 5 s. Calcular la distancia total recorrida.
Datos:
M.R.U.A
Vo= 0
a=4 m/s2
t= 8 s
X1=?
M.R.U
t= 6 s
X2=?
Vf=0
t=5 s
X3=?
Xtotal= ?
1er Movimiento:
M.R.U.A
Vo= 0
a=4 m/s2
t= 8 s
X1=?
X1= Vo*t + a*t2 /2
X1=0 m/s * 8 s + 4 m/s2 * (8s)2/2
X1= 0 m + 128 m
X1=128 m
Vf= Vo + a*t
Vf= 0 m/s + 4 m/s2 *8 s
Vf= 0 m/s + 32 m/s
Vf= 32 m/s
Esta Vf es la velocidad inicial del otro movimiento; ya que el movimiento es uniforme y la velocidad permanece constante
2do Movimiento:
M.R.U
X= V*t
X= 32 m/s * 6 s= 192 m
3er Movimiento:
Vo= 32 m/s
Vf= 0 m/s
t= 5 s
a=?
X3=?
a=Vf – Vo/t
a= 0 m/s – 32 m/s/5s
a= -6,4 m/s2
X3= Vo*t + a*t2 /2
X3=32 m/s * 5 s + (-6,4m/s2 )* (5s)2/2
X3= 160 m - 80 m
X3=80 m
Xtotal = X1 + X2 + X3

UNIDAD 3. CONDENSADORES
Definición , Unidades y Formulas:
En electricidad y electrónica, un condensador (del latín "condensare") es un dispositivo que almacenaenergía eléctrica, es un componente pasivo. Está formado por un par de superficies conductoras en situación de influencia total (esto es, que todas las líneas de campo eléctrico que parten de una van a parar a la otra), generalmente en forma de tablas, esferas o láminas, separadas por un material dieléctrico (siendo este utilizado en un condensador para disminuir el campo eléctrico, ya que actúa como aislante) o por elvacío, que, sometidas a una diferencia de potencial (d.d.p.) adquieren una determinada carga eléctrica, positiva en una de las placas y negativa en la otra (siendo nula la carga total almacenada).
La carga almacenada en una de las placas es proporcional a la diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad la llamada capacidad o capacitancia. En el Sistema internacional de unidades se mide en Faradios (F), siendo 1 faradio la capacidad de un condensador en el que, sometidas sus armaduras a una d.d.p. de 1 voltio, éstas adquieren una carga eléctrica de 1 culombio.
La capacidad de 1 faradio es mucho más grande que la de la mayoría de los condensadores, por lo que en la práctica se suele indicar la capacidad en micro- µF = 10-6, nano- nF = 10-9 o pico- pF = 10-12 -faradios



No hay comentarios.:
Publicar un comentario