INFORMATICA 2BGU "E"

PUNTOS DE UN TRIANGULO

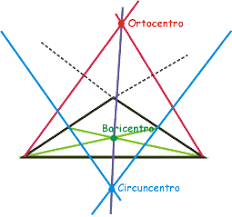
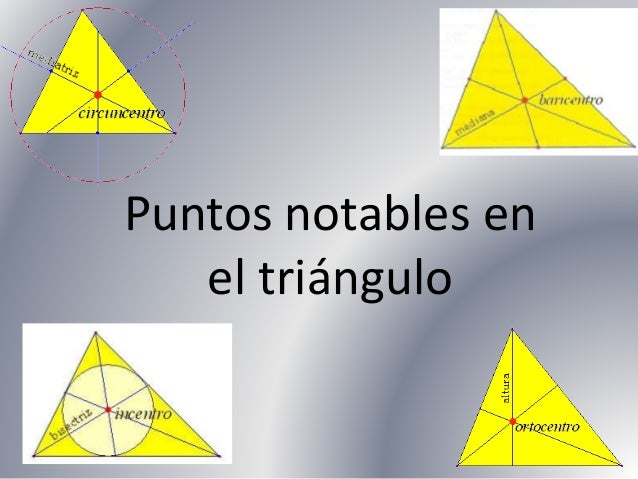
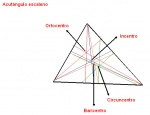
Rectas y puntos notables de un triángulo. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo. Dos lados contiguos forman uno de los ángulos interiores del triángulo. En los triángulos se puede denotar un grupo de rectas y puntos muy importantes. Entre las rectas notables más conocidas de un triángulo se pueden nombrar las mediatrices, las medianas, las alturas y las bisectrices; cada una de estas rectas notables determina cierto punto notable: circuncentro, baricentro, ortocentro e incentro, respectivamente.

                                

Sumario

 [ocultar] 

• 1 Mediatriz
  • 1.1 Mediatrices de un triángulo obtusángulo
  • 1.2 Meditrices de un triángulo rectángulo
• 2 Mediana
• 3 Las Alturas
  • 3.1 El ortocentro en un triangulo obtusángulo
• 4 Las bisectrices
• 5 Generalidades
• 6 Fuentes
•              
•  

Mediatriz

                               

Mediatriz: Conjunto de puntos del plano que equidistan de los puntos extremos de un segmento. Como consecuencia la mediatriz biseca perpendicularmente al segmento.

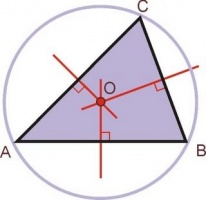
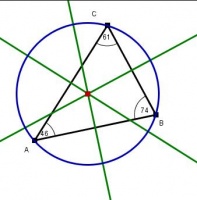
 En un triángulo, las tres mediatrices de sus lados concurren en un punto que equidista de los vértices del triángulo. El punto en el que se cortan las mediatrices de un triángulo, se conoce como circuncentro, o sea, el centro de la circunferencia circunscrita al triángulo de referencia. Al radio de la circunferencia circunscrita se le suele llamar circunradio y es la distancia desde el circuncentro a los vértices del triángulo. Obviando el rigor de la definición de círculo, a la circunferencia circunscrita se le llama también circuncírculo (para abreviar).

mediatríz

• En el triángulo ABC las mediatrices MAC, MBC y MAB se intersecan en el punto C que costituye el circucentro del triángulo o centro de la circunferencia circunscrita al triángulo ABC.

Mediatrices de un triángulo rectángulo

Mediatrices de un triángulo obtusángulo

• En el caso de los triángulos obtusángulos, el circuncentro es un punto ubicado fuera del triángulo.

Mediatrices de un triángulo obtusángulo

Meditrices de un triángulo rectángulo

• En el caso de los triángulos rectángulos, el circuncentro es el punto medio de la hipotenusa

Mediana

Mediana:

                                

• La mediana es el segmento de recta que se traza desde un vértice de un triángulo al punto medio de su lado opuesto.
• Las tres medianas de un triángulo concurren en un punto.
• El punto donde se cortan la medianas de un triángulo se conoce como baricentro, centroide o centro de gravedad y tiene una propiedad física muy importante: Si colocamos un eje a través de él y dejamos libre el triángulo, este no se mueve por acción de la aceleración de la gravedad, es por ello que el baricentro se llama centro de gravedad del triángulo.
• Las medianas se cortan siempre en un punto interior al triángulo.
• El baricentro divide a cada mediana en la razón 2:1. Esto es, la longitud del segmento de mediana medida desde el vértice al baricentro es el doble que desde el baricentro al punto medio del lado en cuestión.
• Cada mediana de un triángulo, lo divide en dos triángulos de igual área.

Mediana

Las Alturas

• Se llama altura de un triángulo al segmento de perpendicular trazada por un vértice del triángulo y comprendido entre ese vértice y su lado opuesto.

• Las alturas de un triángulo concurren en un punto denominado ortocentro del triángulo.

• El ortocentro de un triángulo acutángulo es un punto interior del triángulo.

El ortocentro en un triangulo obtusángulo

• En el caso de un triángulo obtusángulo, el ortocentro es un punto exterior al triángulo.

Archivo:Ortocentro obtusangulo.JPG

• En el caso del triángulo rectángulo vemos que el ortocentro coincide con el vértice del ángulo recto.

• Los pies de las alturas de un triángulo determinan un triángulo llamado: triángulo pedal u órtico del triángulo dado.

Las bisectrices

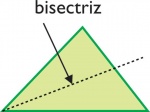
• Bisectriz de un ángulo: Es el conjunto de puntos del plano donde está contenido el ángulo que equidista de los lados del ángulo. Como consecuencia la bisectriz de un ángulo lo divide en dos ángulos de igual amplitud.

• Todo ángulo tiene dos bisectrices, una interna y otra externa. Las bisectrices interna y externa de un ángulo son perpendiculares entre sí.

• Las bisectrices de los ángulos interiores de un triángulo concurren en un punto que equdista de los lados del triángulo, llamado incentro del triángulo o centro de la circunferencia inscrita en el triánguloy siempre es interior al triángulo. La equidistancia se llama inradio o radio de la circunferencia inscrita en el triángulo.

• Cada bisectriz interna y las bisectrices de los otros dos ángulos externos del triángulo concurren en otros tres puntos que también equidistan de los lados (o sus prolongaciones) del triángulo. Estos puntos se llaman exincentros del triángulo y las circunferencias que determinan: circunferencias exinscritas del triángulo. Algunos autores las llaman circunferencias excritas o excírculos y a sus centros excentros.

Generalidades

• Una ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto a este. También se la conoce como transversal angular.La mediana, la altura y la bisectriz son cevianas. El nombre de ceviana fue introducido por M.A. Poulain, que lo introdujo en honor de Giovanni Ceva, quien en 1678 había formulado el teorema que lleva su nombre: Teorema de Ceva. Este teorema da la condición necesaria y suficiente para que tres cevianas se corten en un punto.

• En el triángulo equilátero coinciden todas las rectas y puntos notables tratados, es decir, las medianas, las alturas, las bisectrices y las mediatrices, así como el baricentro, el ortocentro, el incentro y el circuncenro.

• En el triángulo isósceles la altura relativa a la base, es mediana, bisectriz y mediatriz.

• El ortocentro de un triángulo coincide con el incentro de su triángulo pedal.

• Se conoce como circunferencia de los nueve puntos a una circunferencia que se puede construir sobre cualquier triángulo dado. Su nombre deriva del hecho que la circunferencia pasa por nueve puntos notables, seis de ellos sobre el mismo triángulo (excepto que el triángulo sea obtusángulo). Estos nueve puntos son: el punto medio de cada lado del triángulo, los pies de las alturas, y los puntos medios de los segmentos determinados por el ortocentro y los vértices del triángulo. A la circunferencia de los nueve puntos se le conoce también entre otros como circunferencia de Feuerbach, circunferencia de Euler, etc.

• Existen otras rectas y puntos notables del triángulo, a saber:

• La recta de Simson, las simedianas y puntos simedianos,, punto, ángulo y circunferencia de Brocard, la recta de Gauss, el punto de Miquel, la circunferencia de Lemoine, etc.

• Son teoremas importantes relacionados con las rectas y puntos notables del triaángulo, colinealidad de puntos o concurrencia de rectas, los teoremas Carnot, de Ceva, de Menelao, de Feuerbach, de Desargues, de Stewart, de Steiner, de Spieker, etc.